Materi Matematika Numerik - Persamaan Diferensial

Persamaan Diferensial

Persamaan diferensial adalah suatu persamaan yang memuat turunan terhadap satu atau lebih dari variabel-variabel bebas (independent variables). Bila hanya ada satu variabel bebas yang diasumsikan, maka subyek disebut persamaan diferensial biasa (ordinary differential equation). Contoh persamaan diferensial biasa sebagai berikut :

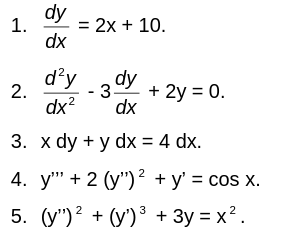
contoh persamaan diferensial

Jika pada persamaan diferensial ada dua atau lebih variabel bebas dan memuat turunan parsial maka dinamakan persamaan diferensial parsial (partial differential equation). Sebagai contoh:

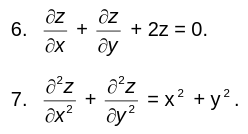
Contoh persamaan diferensial parsial

Untuk selanjutnya tulisan ini hanya membahas persamaan diferensial biasa.

Sejarah Persamaan Diferensial

Persamaan diferensial pertama kali eksis dengan penemuan kalkulus oleh Newton dan Leibniz. Pada bab 2 hasil karyanya tahun 1671 berjudul "Methodus fluxionum et Serierum Infinitarum",Isaac Newton menuliskan 3 macam persamaan diferensial:

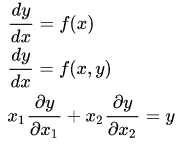
3 macam persamaan diferensial oleh Isaac Newton

Jacob Bernoulli mengusulkan persamaan diferensial Bernoulli tahun 1695.Hasilnya berupa persamaan diferensial biasa dalam bentuk :

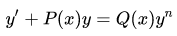
versi jacob bernoulli

dimana pada tahun berikutnya Leibniz mendapatkan penyelesaian dengan menyederhanakannya.

Secara historis, masalah senar bergetar seperti instrumen musik dipelajari oleh Jean le Rond d'Alembert, Leonhard Euler, Daniel Bernoulli, dan Joseph-Louis Lagrange. Tahun 1746, d’Alembert menemukan persamaan gelombang satu dimensi, dan 10 tahun kemudian Euler menemukan persamaan gelombang 3 dimensi.

Persamaan Euler–Lagrange dikembangkan tahun 1750-an oleh Euler dan Lagrange sehubungan dengan studi mereka mengenai masalah tautokron. masalah ini adalah menentukan kurva dimana partikel berbobot akan jatuh pada titik tertentu pada waktu tertentu, tidak tergantung dari titik awal. Lagrange menyelesaikan masalah ini tahun 1755 dan mengirim penyelesaiannya ke Euler. Keduanya kemudian mengembangkan metode Lagrange dan mengaplikasikannya ke mekanika, yang akhirnya membentuk perumusan mekanika Lagrangian.

Fourier mempublikasikan kerjanya mengenai aliran panas dalam Théorie analytique de la chaleur (Teori Analisis Panas), yang dimana didasarkan pemikirannya pada hukum pendinginan Newton, yaitu aliran panas antara 2 molekul berdekatan berbanding lurus dengan perbedaan temperatur. Termasuk di dalam buku ini adalah proposal Fourier mengenai persamaan panas untuk difusi panas konduktif. Persamaan diferensial parsial ini sekarang dipelajari oleh siswa fisika matematika.

Persamaan Diferensial Orde Satu

Persamaan Diferensial orde satu adalah suatu fungsi yang memuat satu variabel bebas (x) dan satu variabel tak bebas (y) beserta turunan pertamanya (y′) yang dikaitkan secara eksplisit atau implisit. Solusi umum PD adalah fungsi yang memuat konstanta C dan memenuhi PD tersebut. ``Solusi khusus` adalah solusi yang diperoleh dari solusi umum dengan mengambil nilai C suatu bilangan tertentu atau solusi yang memenuhi syarat yang diberikan, misalnya syarat awal. Grafik dari solusi umum merupakan keluarga lengkungan, di mana untuk setiap nilai C diperoleh suatu lengkungan (kurva) atau trayektori. PD yang solusi umumnya diberikan oleh fungsi g(x,y,C) = 0 dapat ditentukan dengan mengeliminasi C dari kedua persamaan:

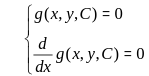
contoh

dengan mengingat y sebagai fungsi dari x.

Definisi 1

Suatu PD orde satu dapat dinyatakan secara umum dalam dua bentuk, yaitu:

Bentuk implisit,

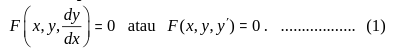
bentuk implisit

Bentuk eksplisit,

bentuk eksplisit

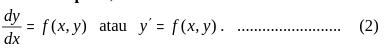
Contoh-contoh mengidentifikasi PD orde satu:

contoh-contoh PD

Definisi 2

Suatu fungsi y = y(x) dikatakan solusi PD (1) atau (2) apabila y = y(x) dan turunannya y′ memenuhi PD (1) atau (2).
definisi dua

Keluarga Lengkungan (Kurva)

Anda telah mengetahui solusi umum suatu PD memuat konstanta C. Jadi solusi umum dapat ditulis dalam bentuk y=y(x,C).

Solusi umum PD: cosyx′= adalah ( , )sinyy x Cx C==+. Grafik dari solusi umum ( , )yy x C= merupakan keluarga lengkungan (kurva) karena untuk setiap pengambilan nilai C diperoleh suatu lengkungan solusi khusus.

keluarga lengkungan

Persamaan Diferensial homogen( homogenousD E )

PD orde satu dalam bentuk y'= f ( x,y ) dikatakan homogen jika, untuk sebarang bilangan real t,berlaku : f(tx,ty)=f(x,y)

Persamaan Diferensial terpisahkan( separable DE )

Bentuk umum:

A(x) dx + B(y) dy = 0

Solusi:

solusi

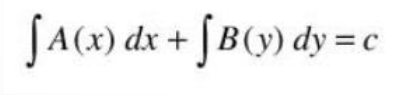
Problem nilai batas

Jika PD disertai dengan kondisi dimana fungsi dan turunannya diberikan nilai pada variabel bebas yang berbeda, maka kondisi ini disebut problem nilai batas